Bubbles, Drops, and Particles in Non-Newtonian Fluids

Chapter 1: Non-Newtonian Fluid behaviour

Classification of Fluid behaviour

Definition of a non-Newtonian fluid

Newtonian fluid

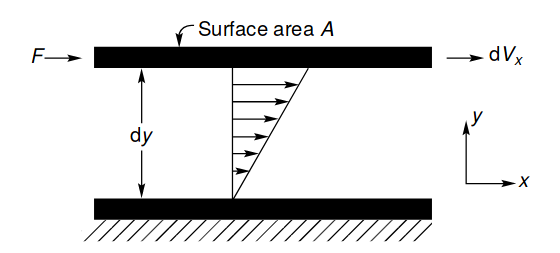
Consider an incompressible fluid in laminar flow sandwiched between two flat plates. When a force is applied to the plate, due to internal friction the fluid exerts an equal force in opposing direction. The opposing force takes the form of shear stress and can be expressed as the product of the viscosity of the fluid and it’s rate of shear.

$$\begin{array}{r}\frac{F}{A}={\tau }_{yx}=\mu \underset{\text{Shear rate}}{\underbrace{\left(-\frac{d{V}_x}{dy}\right)}}=\mu {\dot{\gamma }}_{yx}\end{array}\text{\hspace{1em}(1.1)}$$

• The subscripts in ${\tau }_{yx}$ and ${\dot{\gamma }}_{yx}$ denote the direction normal to the shearing force and the the direction along the force respectively.
• The shear rate is nothing but the velocity gradient of flow in the direction perpendicular to the force.
• The negative sign implies that the Shear stress acts in the direction opposite to the force.

Newtonian Viscosity (Dynamic viscosity) $\mu$ is independent of Shear rate and Shear stress. It only depend on pressure and temperature of the fluid.

Flow curve / Rheogram is the graph of Shear stress against Shear rate. For a Newtonian fluid, the slope of a Rheogram is constant .i.e $\mu$ is constant, thus giving a straight line.

For an incompressible fluid $(1.1)$ can be written as

$${\tau }_{yx}=\frac{\mu }{\rho }\left(-\frac{d\rho V_x}{dy}\right)$$

• Where "$\rho V_x$" is the momentum transfer per volume in $y$-direction.
• Thus the "${\tau }_{yx}$" term also represents the momentum flux in $y$-direction.
• $-ve$ sign implies that the momentum transfer is in the direction of decreasing velocity.
• This is in line with Fourier’s law of heat transfer and Fick’s law of diffusive mass transfer

Simple Shear flows are flows where the velocity of the fluid has only 1 component and varies only in 1 direction.

• For simple shear flows the Deviatoric Stress components are identically zero.

$${\tau }_{xx}={\tau }_{yy}={\tau }_{zz}=0\text{\hspace{1em}(1.9)}$$

• For a fluid to be Newtonian, $\mu$ has to be constant and additionally the deviatoric stress components also must be zero.
• Fluids that have a constant viscosity but don’t have zero deviatoric stresses are called 220410 Boger fluids

Non-Newtonian fluid behaviour

A non-Newtonian fluid is one whose flow curve is not linear and does not pass through the origin. The ratio of the shear stress to the shear rate of the fluid is therefore called apparent viscosity, which is not constant for a given temperature and pressure and is in turn dependant on the flow conditions (flow geometry, shear rate etc).

Three types of non-Newtonian fluid:

• Generalised Newtonian fluid is one where the shear rate at any point is determined by the value of shear stress at that point, at that particular instant of time i.e, it is not dependant on the history of deformation ¹. They also go by names ‘time independent’, ‘purely viscous’ or ‘inelastic’ fluids.
• Time-dependant fluid is one where the relationship between shear stress and shear rate depends on the duration of shearing and the kinematic history of the fluid.
• Visco-elastic fluids is one where the fluid exhibits both viscous and elastic characteristics when undergoing deformation. Thus it has characteristics of an idealised fluid as well as an elastic solid. These fluids often show partial elastic recovery.

Most real-world fluids however do not purely fall under a particular category. They often exhibit a mixture of these characteristics and in the dominant characteristic is identified and used as a base for analysis.

Time-independent fluid behaviour

Shear-thinning or Pseudoplastic fluid Viscoplastic Shear-thickening or dilatant

Time-dependant fluid behaviour

Thixotropy Rheopexy or negative Thixotropy

Visco-elastic fluid behaviour

A visco-elastic fluid exhibits properties of a perfect-solid (elastic) and a Newtonian fluid (constant viscosity) For a perfect solid deformed elastically, the material will regain it’s original shape once the shearing force is removed. However, once a particular yield stress is reached, complete recovery is not possible and ‘creep’ takes place i.e, the solid will have flowed.

Many materials show both elastic and viscous behaviour. However, we only observe the elastic or viscous properties in practice and hence even though these conditions are limiting, they go unnoticed. If the state of a material is dependent on it’s response to it’s behaviour when subjected to force, then it is true that we have to consider not only the structure of the material, but also on the kinematic conditions to which it has been subjected. Thus the distinction between solid (elastic) and fluid (viscous) is arbitrary to some extent.

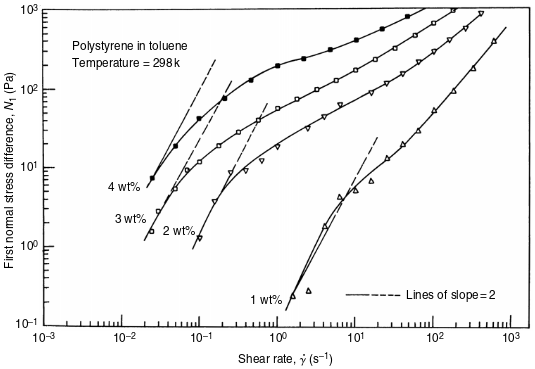
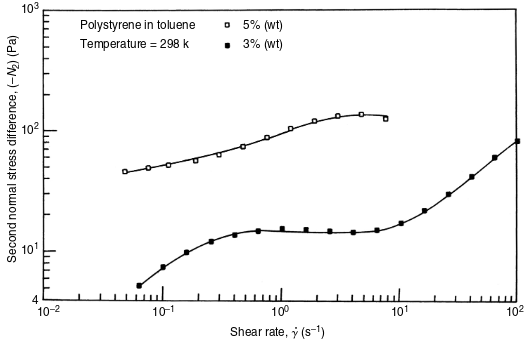
Normal Stresses in steady shear flows

• The shearing of a Viscoelastic fluid gives rise to unequal normal stresses.

$$P_{xx}\ne P_{yy}\ne P_{zz}$$

• The difference between the normal stresses are easier to measure and are defined as

$$\begin{array}{rl}& \text{Primary normal stress difference, }{N}_1=P_{xx}-P_{yy}\\ & \text{Secondary normal stress difference, }{N}_2=P_{yy}-P_{zz}\end{array}$$

• Coupled with the shear rate, the normal stress difference is useful in describing the rheological properties.

$$\begin{array}{rl}& \text{Primary normal stress coefficient, }{\psi }_1=\frac{N_1}{({\dot{\gamma }}_{yx}{)}^2}\\ & \text{Secondary normal stress coefficient, }{\psi }_2=\frac{N_2}{({\dot{\gamma }}_{yx}{)}^2}\end{array}$$

• Normal stress Difference in action
  • $N_1$
  • $N_2$

Elongational flow Flow that results due to the stretching of fluids in one or more directions. 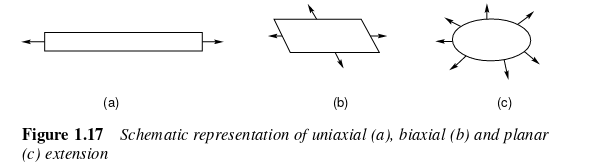For an incompressible fluid in elongational flow the volume of the element must remain constant. Hence, rate of elongation $\dot{ϵ}$ in $x-$direction is accompanied by contraction in $y$ and $z$ directions. Assuming the contractions are symmetric, components of velocity are given by

$$V_x=\dot{ϵ}x,V_y=-\frac{\dot{ϵ}}{2}y,\text{ and }{V}_z=-\frac{\dot{ϵ}}{2}z\text{\hspace{1em}(1.22)}$$

Rate of elongation in $x-$direction

$$\dot{ϵ}=\frac{\partial V_x}{\partial x}\text{\hspace{1em}(1.23)}$$

Elongational viscosity for uniaxial extension, the

$${\mu }_E=\frac{P_{xx}-P_{yy}}{\dot{ϵ}}=\frac{{\tau }_{xx}-{\tau }_{yy}}{\dot{ϵ}}\text{\hspace{1em}(1.24)}$$

Footnotes

1. https://en.wikipedia.org/wiki/Generalized_Newtonian_fluid ↩