Residuals in CFD

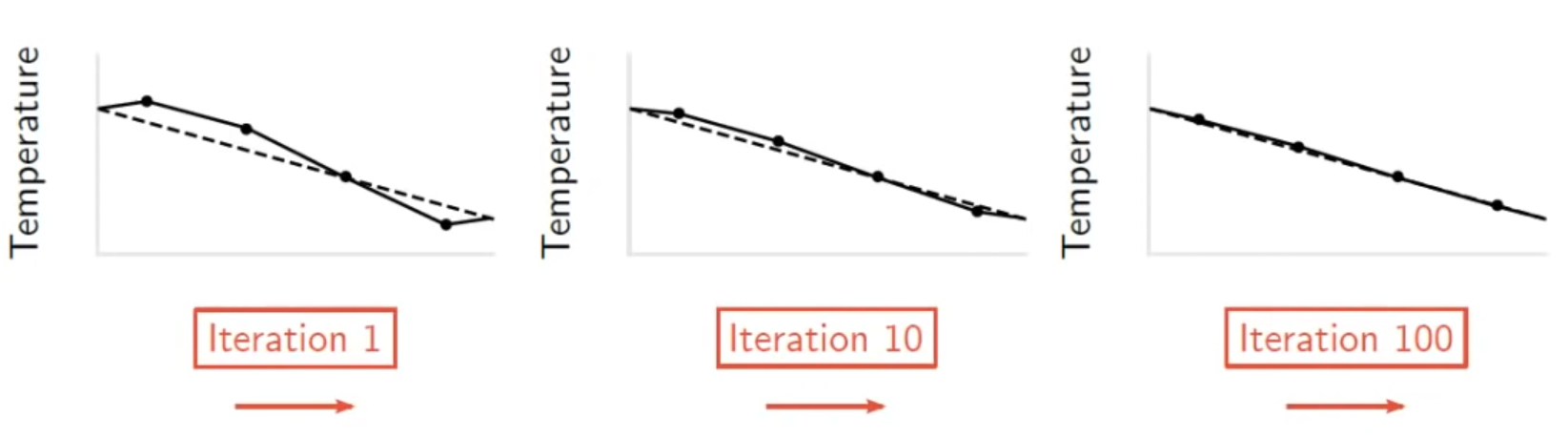
• CFD codes use iterative approach to solve the solution matrix.
• Consider a CFD solution of Heat conduction in a 1D bar without a heat source.

• The solution matrix for a bar with 5 cells

$$AT=B$$

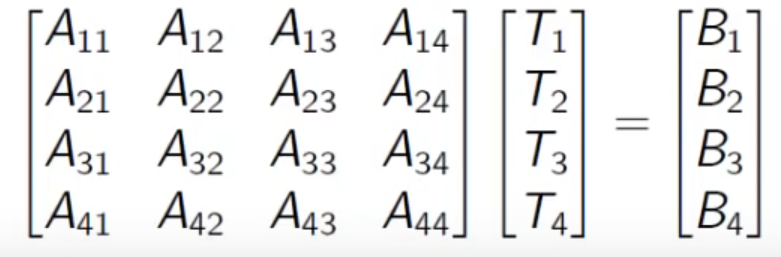
$A\to$ Heat flux gradient, $T\to$ Temperature & $B\to$ Heat source

• The Matrix equation for residual is defined as

$$AT-B=r$$

• Once the Temperature field is calculated, each value can be substituted and the residuals can be obtained.
• As $r\to 0$, the solution gets more accurate.
• From the matrix definition, the residual is vector give the local error in each cell.
• Note that the residual has the same units as the quantity calculated by the solution algorithm.
• In general

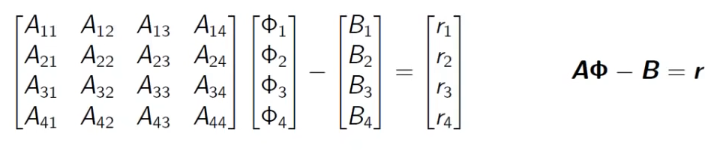
Representative Residual

The residual vector contains the error for every cell in the mesh, making it impractical to monitor against iteration. A representative residual is a scalar that represents the residual for all cells in the mesh.

Three Norms for Calculating Residuals

1. $L_1$ Norm

• Also known as the mean of all residual components
• Has no bias

$r=\frac{1}{N}{\sum }_{i=0}^n|r_i|$

2. $L_2$ Norm

• Mean magnitude of all components of the residual vector
• Approximately equivalent to RMS (Root Mean Square)
• Biased towards large values
• Magnifies the effect of a few bad cells on the representative residual

$r={\left(\frac{1}{N}{\sum }_{i=0}^n|r_i{|}^2\right)}^{1/2}$

3. $L_{\infty }$ Norm

• Takes the maximum of the residual vector

$r=\text{max}|r_i|$

References

1. https://www.youtube.com/watch?v=v9OnNeYH4Ok&