Gauss's Divergence Theorem(L)

Gauss’s Divergence Theorem

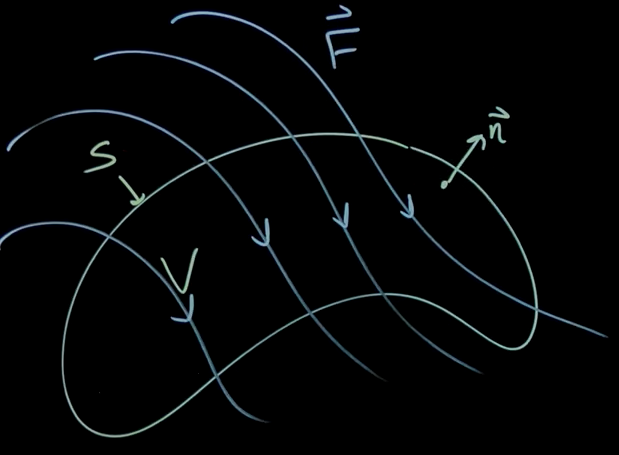
Definition: The flux of a vector field $\vec{F}$ through a closed surface $S$ is equal to the integral of the divergence $\nabla \cdot \vec{F}$ over the entire enclosed volume $V$.

$$\boxed{\int \int {\int }_{V}dV=\int {\int }_S\vec{F}\cdot \vec{n}dS}$$

Why it’s true The local divergence in the every point in the field may be represented as follows

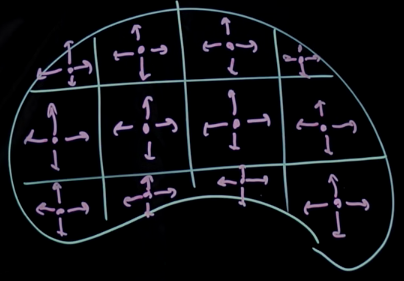
• Assuming the vector field is continuous, and the grid is infinitesimally fine, the fluxes in the opposite direction of each neighbour-owner pair, cancel each other out.
• When each sub volume is integrated, the only divergence vectors that remain belong to the cells without neighbours i.e. along the surface.
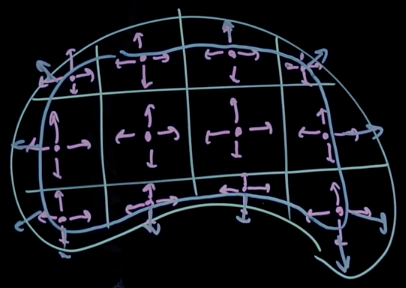
• Note: The integral of all the divergence vectors along the surface is nothing but the flux through the surface.

I don’t understand this: To calculate the volume of an irregular shape, we can set the divergence as 1 and the surface integral gives us the area.

---

References

1. https://www.youtube.com/watch?v=TORt20_HjMY&t=38s