Introduction
- Blood Suspension of cells in Plasma.
- Behaviour
-
Approximated as Newtonian in a large artery.
-
Non-Newtonian in small diameter arteries (0.02 mm-0.1 mm), at low shear rates ()
-
Flow through a narrow artery has a peripheral layer of Plasma (Newtonian) and a core region of RBCs (non-Newtonian).
-
Velocity profile at a narrow artery cannot be accurately measured using a Newtonian model.
-
For realistic description of blood flow, 2 fluid model is required.1
The velocity profiles in the arterioles having diameter less than 0.1 mm are generally explained fairly by the Casson and Herschel-Bulkley fluid models. However, the velocity profiles in the arterioles whose diameters less than 0.0650 mm do not conform to the Casson fluid model, but, can still be explained by the Herschel-Bulkley model”.2
-
Mathematical Formulation
-
Assumptions
- Artery is axially symmetric with mild stenosis, walls are rigid.
- Flow is laminar, pulsatile and fully developed. (Plug flow in the centre)
- Blood is incompressible.
- Radial velocity is negligibly small for small Hence neglected.
-
Essential Nomenclature
-
Domain
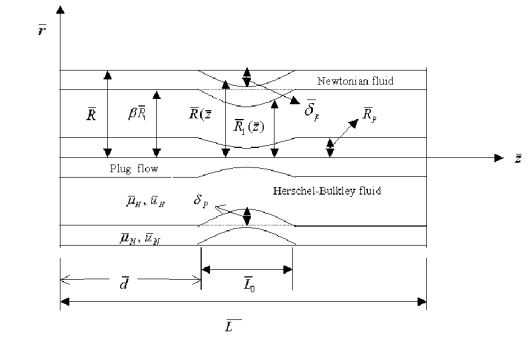 3
3
At , the model reduces to single-fluid model Stenosis at periphery
R coordinates for Peripheral Region
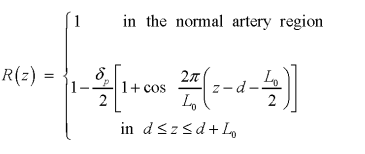 R coordinates for the core region
R coordinates for the core region

- Boundary Conditions
- Because Plug flow is assumed at the center.
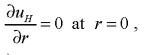
- No slip at wall ( End of stenosed peripheral region)
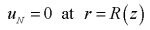
- Interface between core and peripheral regions have same velocity ( end of stenosed core region)
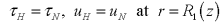
- Temporal Component for Pulsatile behavior (0<A<1, but used 0.2<A<0.5 to pronounce the effect)
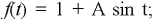
- Inlet velocity as a function of radius
- At Periphery
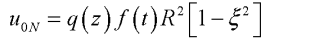
- At core
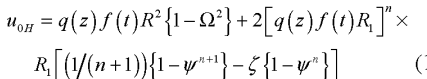
- Pulsatile Reynolds Number ratio
- Reynolds Number
- , but used
- At Periphery
- Because Plug flow is assumed at the center.
- Transport Properties
- Core: 220613 Herschel-Bulkley Equation 10 (s) For n < 1, take n = 0.95 5 For n > 1, take n = 1.05 Healthy: 0.1 << 0.3 Unhealthy: 0.05<<0.15 (yield stress is 5 times in diseased state6)
Footnotes
-
Bugliarello, G, Sevilla, 1., 1970, “Velocity Distribution and Other Characteristics of Steady and Pulsatile Blood Flow in Fine Glass Tubes,” Biorheology, Vol.7, pp. 85~ 107 ↩
-
N., 1978, “Influence of Plasma Layer on Steady Blood Flow in Micro Vessels,” Japanese Journal ofAppliedPhysics, Vol. 17, pp. 203~ 214. ↩
-
V.P. Srivastava, M. Saxena, Two-layered model of Casson fluid flow through stenotic blood vessels: applications to the cardiovascular system, J. Biomech. 27 (1994) 921–928. ↩
-
D.S. Sankar, U. Lee, Two-fluid nonlinear mathematical model for pulsatile blood flow through catheterized arteries, J. Mech. Sci. Technol. 23 (2009) 1650–1669. ↩
-
Sankar D. S., Hemalatha, K., 2006, “Pulsatile Flow of Herschel-Bulkey Fluid Through Stenosed ArteriesA Mathematical Model,” International Journal of Non-Linear Mechanics, Vol. 41, pp. 979~990. ↩
-
S. Chakravarthy, A. Datta, P.K. Mandal, Analysis of nonlinear blood flow in a stenosed flexible artery, Int. J. Eng. Sci. 33 (1995) 1821–1837. ↩