Summed or Composite Quadrature

It is a Quadrature where the domain $x\in [a,b]$ is split into multiple grid points $j=0,1,2\dots J$ with $a=x_0<x_1<\cdots <x_J=b$

$$\boxed{{\int }_a^{b}f(x)\mathrm{d}x=\sum _{j=0}^{J-1}{\int }_{x_j}^{x_{j+1}}f(x)\mathrm{d}x}$$

We sum only till $(J-1)$ because $j=J$ is the end point which means the substitution $x_{J+1}$ doesn’t exist.

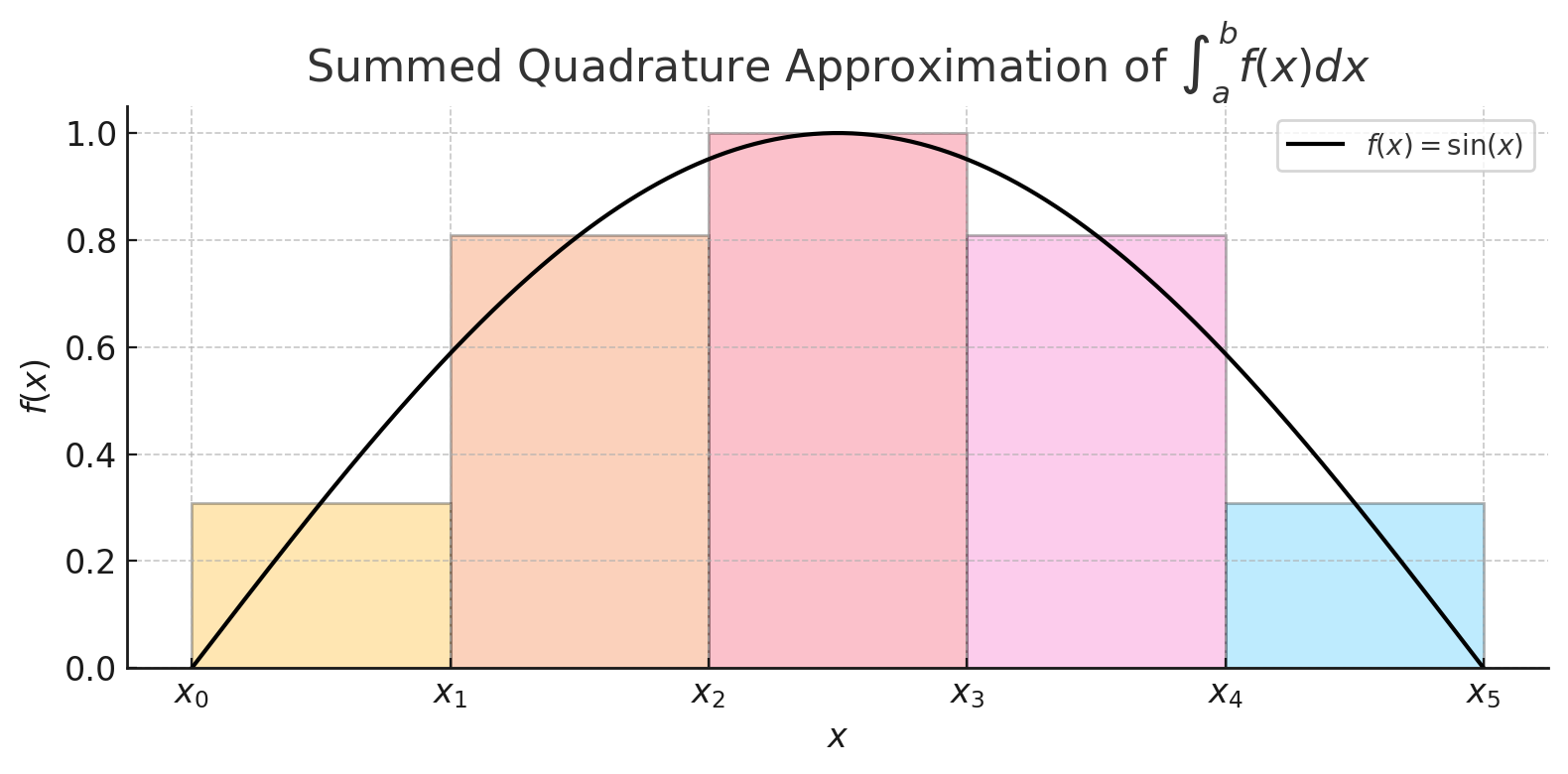
Comparison of Quadrature Rules and their Composite form

Quadrature rule	Composite Quadrature	Fixed Step
Left Rectangle	${\sum }_{j=0}^{J-1}f\left(x_j\right)\left(x_{j+1}-x_j\right)$	$h{\sum }_{j=0}^{J-1}f\left(x_j\right)$
Midpoint	${\sum }_{j=0}^{J-1}f\left(\frac{x_{j+1}+x_j}{2}\right)\left(x_{j+1}-x_j\right)$	$h{\sum }_{j=0}^{J-1}f\left(\frac{x_{j+1}+x_j}{2}\right)$
Trapezoid	${\sum }_{j=0}^{J-1}\left(x_{j+1}-x_j\right)\frac{f\left(x_j\right)+f\left(x_{j+1}\right)}{2}$	$\frac{h}{2}{\sum }_{j=0}^{J-1}\left(f\left(x_j\right)+f\left(x_{j+1}\right)\right)$
Simpson’s		$\frac{h}{6}{\sum }_{j=0}^{J-1}\left(f\left(x_j\right)+4f\left(\frac{x_j+x_{j+1}}{2}\right)+f\left(x_{j+1}\right)\right)$