Exact Differential Equations

Mathematical Definition

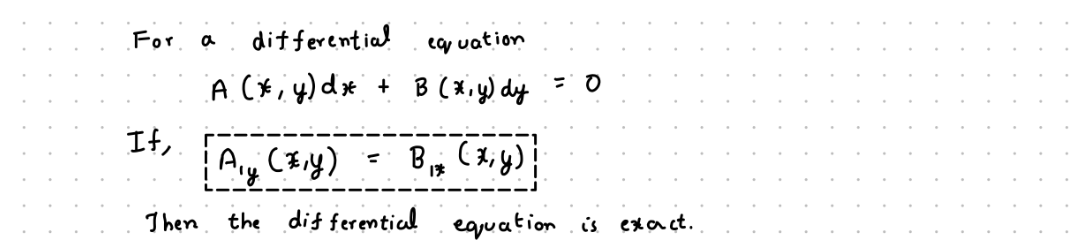
• RHS of the Exact differential equation is zero. This means that the potential function does not change for small step $dx$ and $dy$.
• $A(x,y)=\frac{\partial F}{\partial x}$ and $B(x,y)=\frac{\partial F}{\partial y}$.

Example

Potential function, 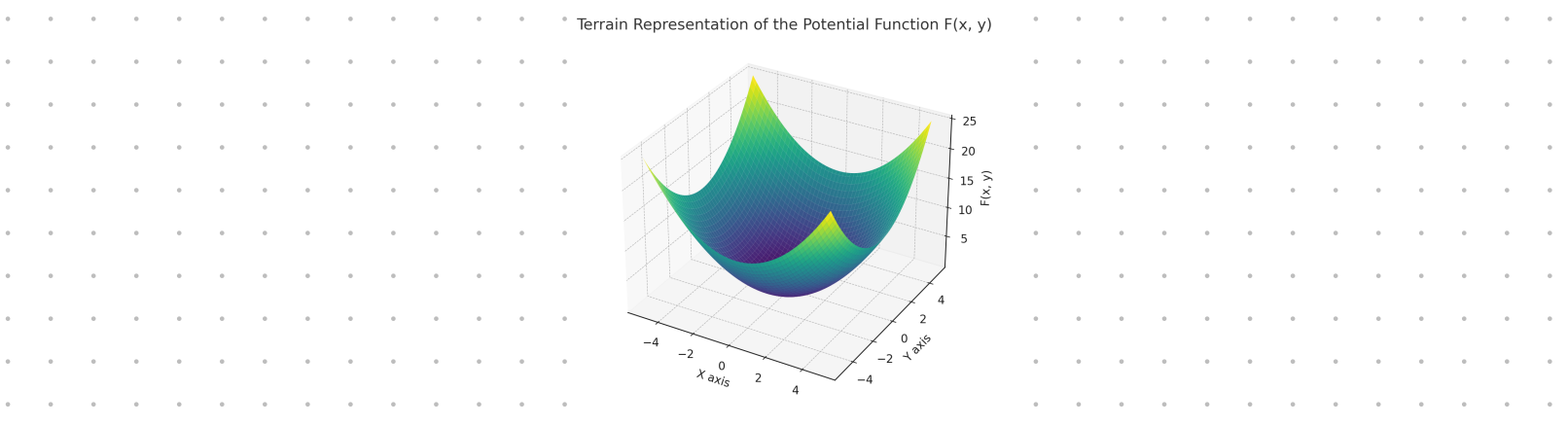$F(x,y)=\frac{1}{2}{x}^2+\frac{1}{2}{y}^2$. The Exact Differential Equation would be the gradient of the function obeying the condition stated above.

$$A(x,y)dx+B(x,y)dy=0$$

where $A(x,y)=\frac{\partial F}{\partial x}=x$ and $B(x,y)=\frac{\partial F}{\partial y}=y$. The Exact Differential Equation

$$xdx+ydy=0$$

Note: The condition $\frac{\partial A}{\partial y}=\frac{\partial B}{\partial x}$, holds.

The path on the solution field of the Potential Function where the value is constant (Constant elevation) is given as follows.

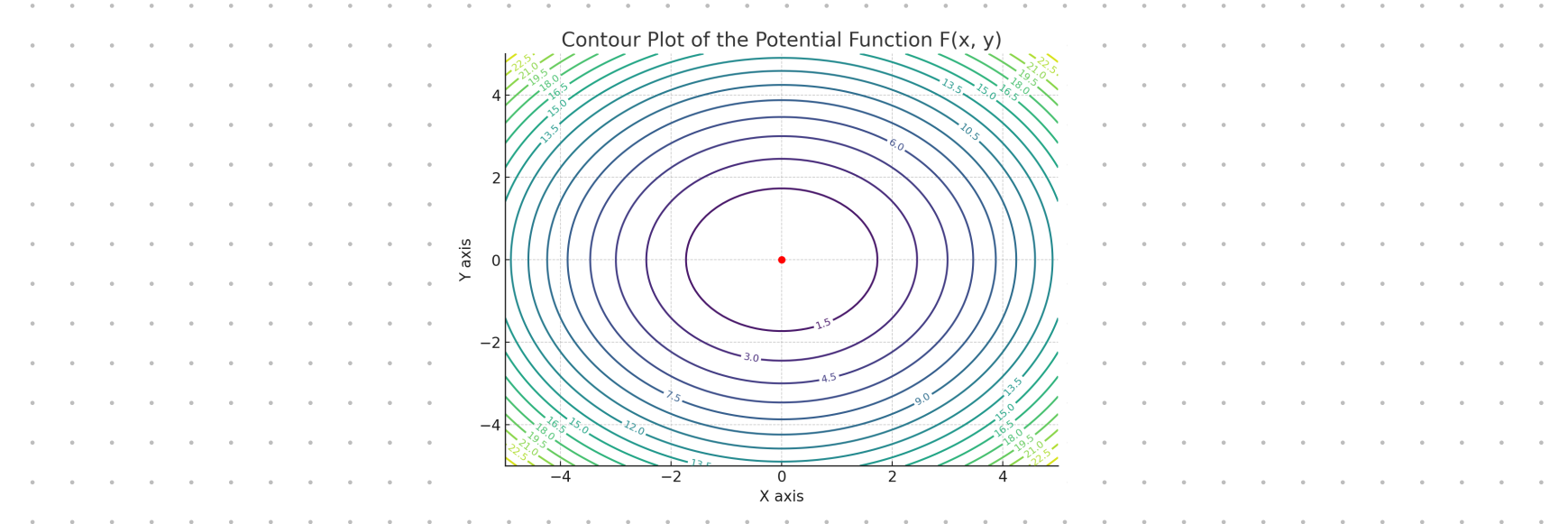
Note: The example chosen was Potential function whose Gradient was known to be an Exact differential equation. In the course, you are asked to build a potential function or verify if a differential equation is exact.