Classification of Parallel Computers
graph TD PS[Parallel System] --> SIMD PS --> MIMD MIMD --> DM[Distributed Memory] DM --> MPP DM --> NOW DM --> Clusters MIMD --> SM[Shared Memory] SM --> UMA SM --> NUMA SM --> COMA NUMA --> ccNUMA NUMA --> ncNUMA
Classification of Memory
Distributed Memory
- Architecture
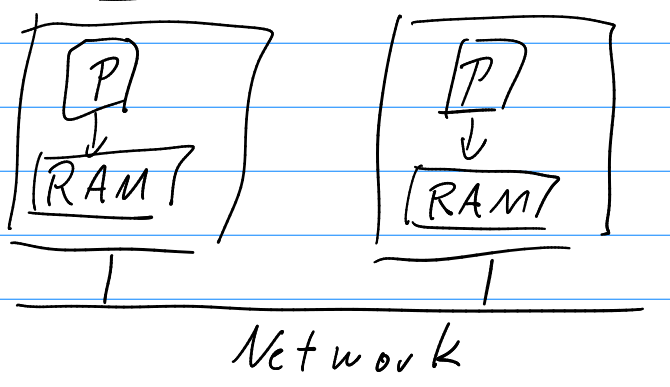
- Programming Model: Message passing.
- Types
- MPP Massive Parallel System
- Specialized system
- Unified Operating system
- Most Super computers run this
- NOW Network of Workstations
- Loosely connected group of individual computers with “standard” network
- Cluster
- Network of Computers with high performance network.
- Separate instance of operating system.
- MPP Massive Parallel System
Shared Memory
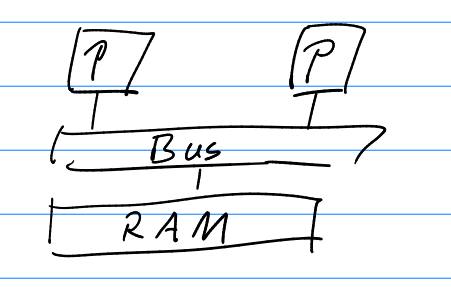
- Programming model: Shared variables.
- Simultaneous access to the same variable is not allowed.
- Types
- NUMA
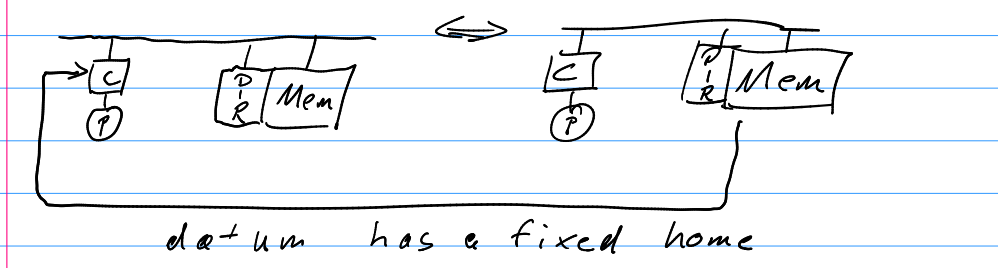
- Each Processor has has a local memory which can be accessed by other processors.
- DIR → Directory. Stores information regarding the files in cache. Like a registry.
- During memory access the DIR is read to know if the file should be accessed from the cache or from memory.
- ccNUMA: Cache Coherent non-Uniform Memory Access
- nccNUMA: non-ccNUMA
- COMA: Cache only memory access
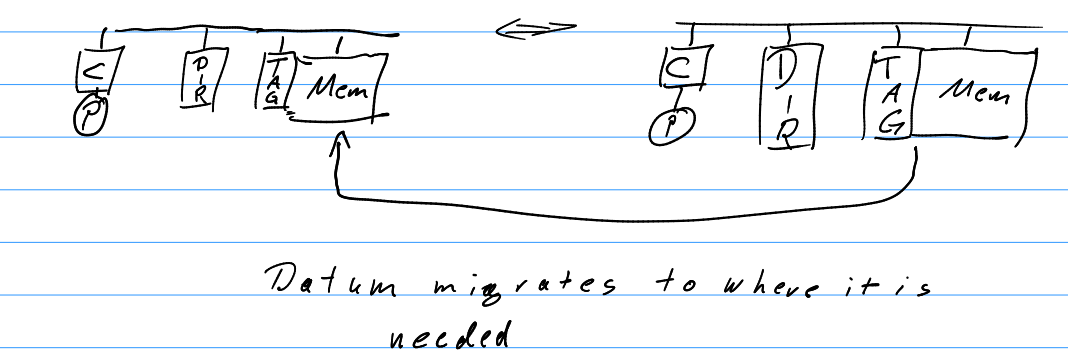
- TAG → It is an identifier for each Datum.
- Datum migrates to where it is needed, hence you need a TAG to identify the data.
- Here the memory is accessed through the cache only.
- This means that this if the same data is being used, the access operation is much faster.
- NUMA
Understanding the architecture is essential to writing efficient programs.
-
Example:
- Caches are accessed in form of cache lines of fixed size - like a bus transporting people, it has the same energy is used to transport 1 person and 100 passengers.
- To avoid Cache misses, data should be processed continuously. (cache miss: it occurs when the program looks at the DIR and doesn’t find what’s required hence it searches for it in memory which is expensive)
-
Code example
for (int i = 0; i < x; i++) { for (int j = 0; j < y; j++) { data1[i + x * j] = func(i, j); // Data 1 data2[j + y * i] = func(i, j); // Data 2 } } -
Loop 1 (Faster) exhibits sequential memory access. As the inner loop increments
j, the expressioni * x + jaccesses consecutive memory locations (k,k+1,k+2, …). This pattern takes full advantage of the cache. After the first access, the next several required data points are already in the fast cache, leading to a high “cache hit” rate. -
Loop 2 (Slower) exhibits strided memory access. As the inner loop increments
j, the expressionj * y + ijumps through memory in large steps (strides of sizey). Each access likely requires fetching a new cache line from slow main memory, causing a “cache miss” on almost every iteration.
Networks
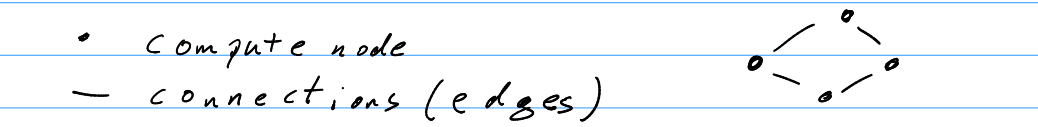
- Distance between nodes
- Shortest path in # edges between two nodes. (#→ number of something )
- Degree
- Largest number of edges at a node.
- Diameter
- Largest distance between two nodes.
Examples
- Fully connected Network
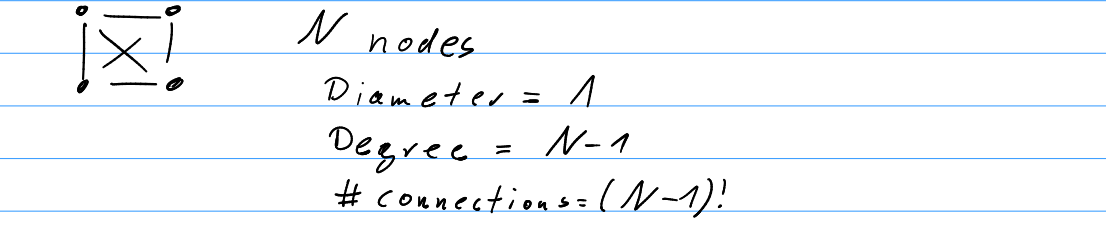
- Linear network
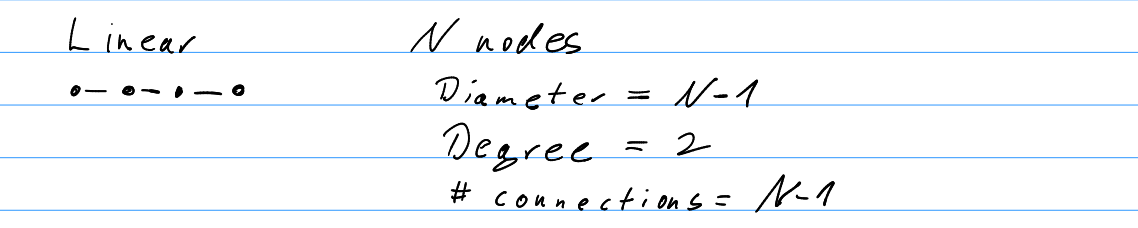
- Ring network or 1D Torus
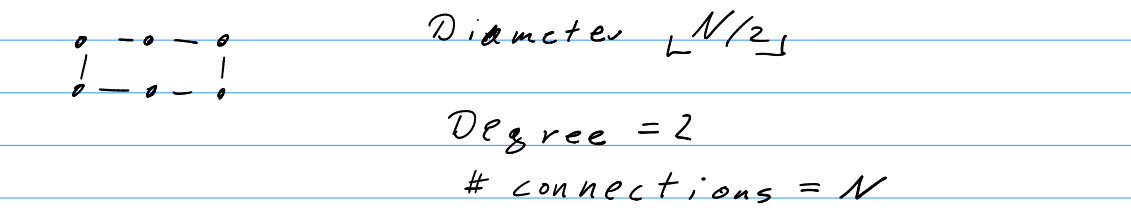
- dD Torus (d→ dimension)
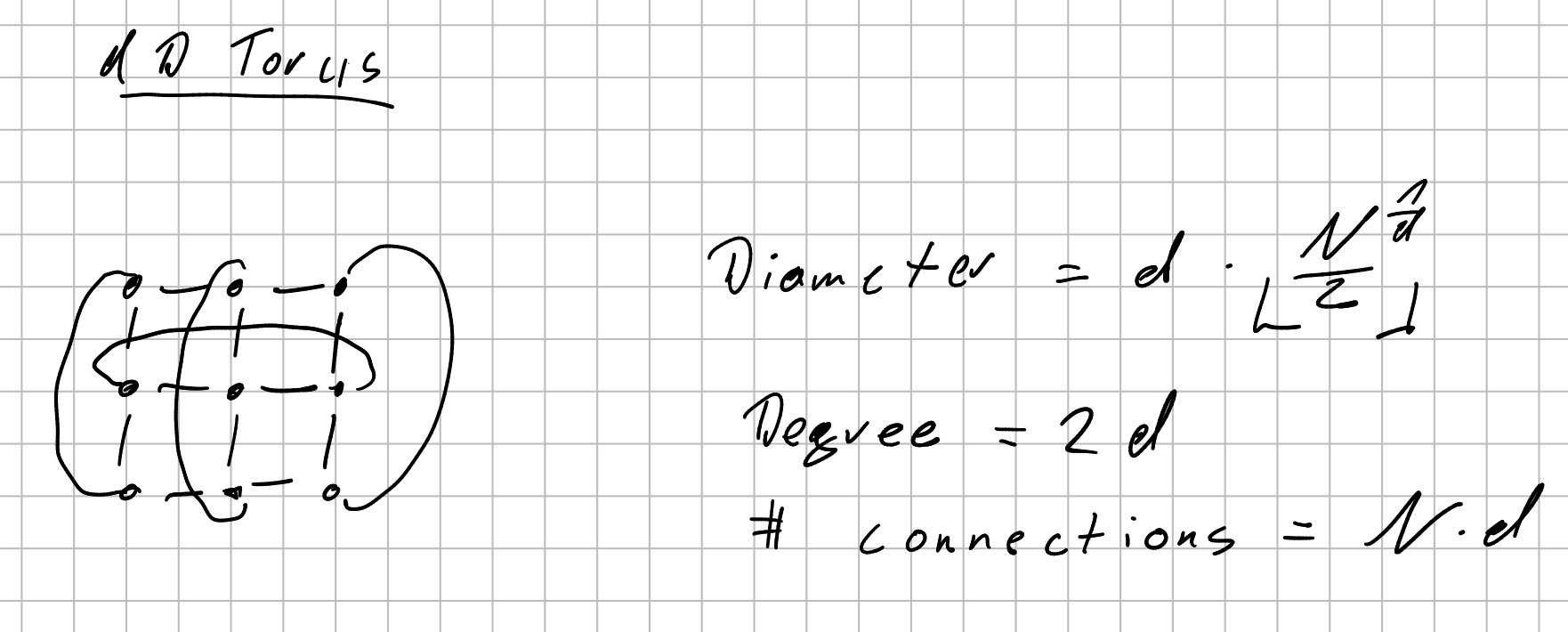
- D-Dimensional hypercube
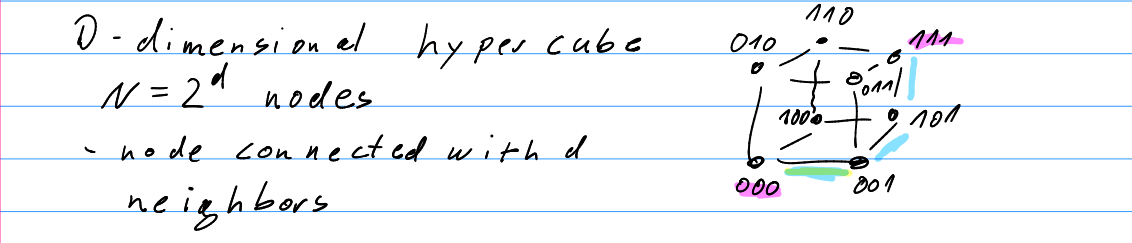
- Diameter = =
- Degree = =
- Nodes
- Node connected with neighbors.
- Indexed by bits.
- Node index differ from neighbor’s index by 1 bit.
- Patch through the network changes bit at a time
- 000→001→101→111
- Distance between nodes = # Bits different in the index
- Hamming Distance: number of non-matching bits two words of same length.(How many bits have to be changed to go from one data to another data.)