Fisher's Linear Discriminant Function

Motivation

We try to find a weight vector $\mathbf{w}$ such that the Hyper Plane is $\perp$ to it.

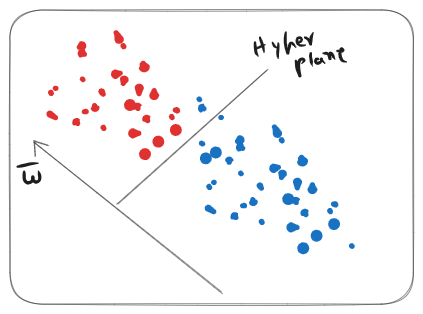
The position of the Hyper Plane however is not known. We can find it using the following methods.

High-level Heuristic for Fisher’s LDF

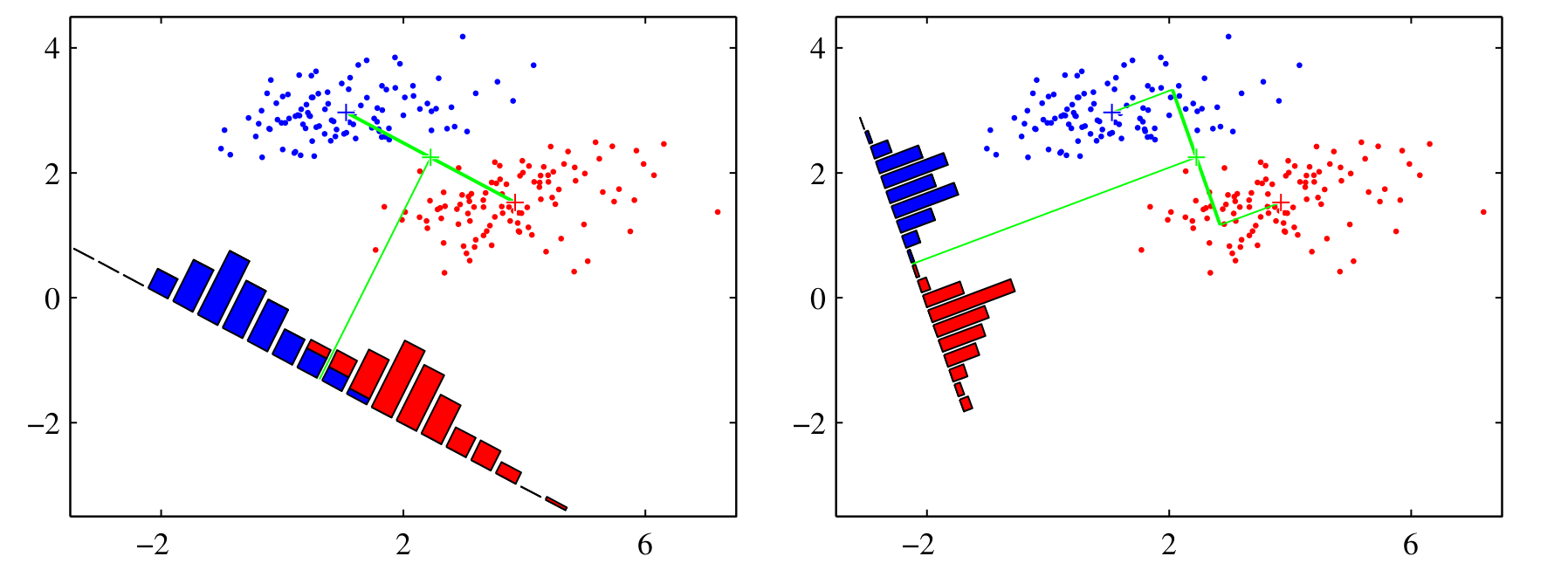
1. Project Data onto a Line: The first step is to calculate the projection of the data onto a line, which is represented by the weight vector.
2. Define the Hyperplane: The discriminant hyperplane (the decision boundary) is orthogonal to the projection line.
3. Optimize the Hyperplane: The position of this hyperplane is then optimized to achieve the best possible separation between the classes.
4. Choose a Threshold: Finally, a threshold value (${\omega }_0$) is selected to be used for the final discrimination between classes

Fisher Criterion

To find the Optimum classification, we maximize the Fisher Criterion. For class mean $m$ and projected line $\mathbf{w}$:

$$w\ast =\arg \underset{\mathbf{w}}{\max }J(w)=\frac{{\left(m_2^{\prime }-m_1^{\prime }\right)}^2}{s_1^2+s_2^2}=\frac{{\left({\mathbf{w}}^T{m}_2-{\mathbf{w}}^T{m}_1\right)}^2}{s_1^2+s_2^2}$$

We do this because it:

• Maximizes Inter-Class Variance: The numerator, ${\left(m_2^{\prime }-m_1^{\prime }\right)}^2$, represents the squared distance between the means of the projected classes. Maximizing this term pushes the centers of the different classes as far apart as possible.
• Minimizes Intra-Class Variance: The denominator, $s_1^2+s_2^2$, represents the sum of the variances within each projected class. By minimizing this term, the criterion ensures that the data points within each class are tightly clustered around their respective centers.

By optimizing both of these objectives at the same time, the Fisher criterion finds a projection that reduces the overlap between the classes, making them easier to separate with a simple threshold.

source