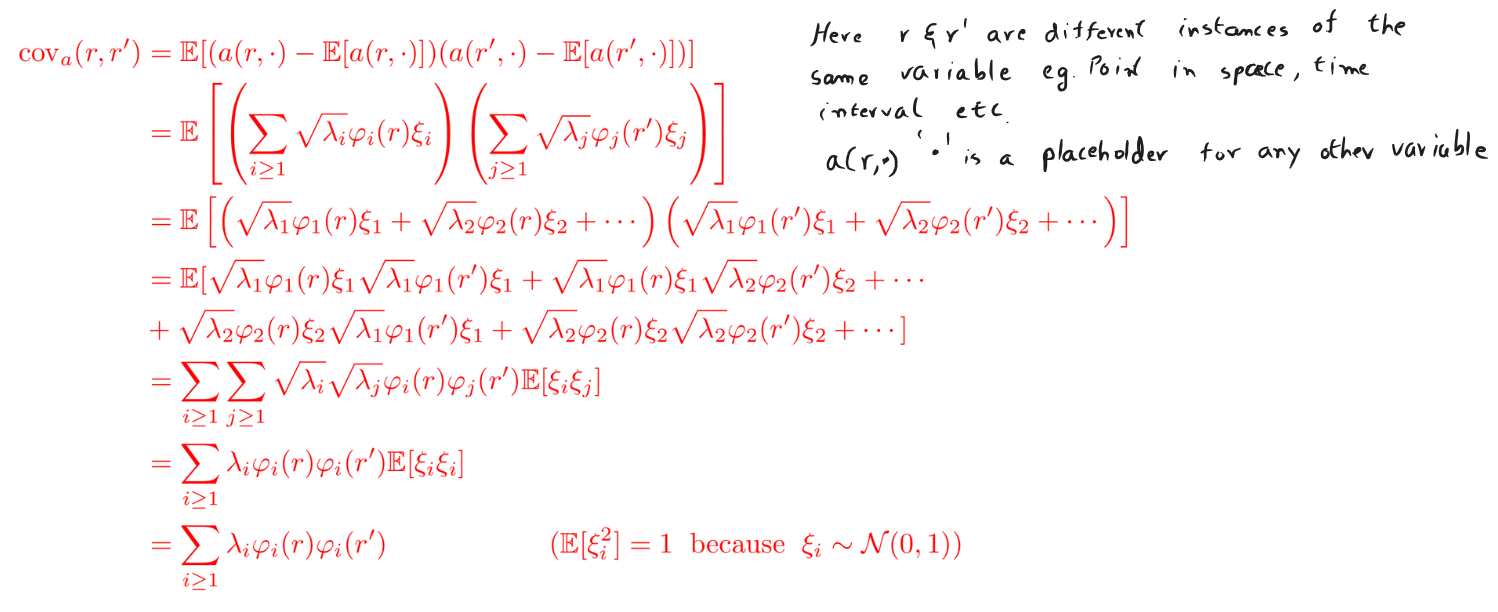Continuous KLE Example

In the following we assume that $a$ is a random process, i.e., $a:\Theta \times \left[a_1,b_1\right]\to$ $\mathbb{R}$ with the Karhunen-Loève expansion

$$a(\theta ,r)={\mu }_a(r)+\sum _{i=1}^{\infty }\sqrt{{\lambda }_i}{\phi }_i(r){\xi }_i(\theta )$$

where ${\lambda }_i,{\phi }_i$ refer to the eigenvalues and eigenfunctions that satisfy the equation ${\int }_{a_1}^{b_1}{\mathrm{cov}}_a\left(r,r^{\prime }\right){\phi }_i(r)dr={\lambda }_i{\phi }_i\left(r^{\prime }\right)$, with ${\mathrm{cov}}_a$ being the covariance function of $a$. For the eigenfunctions, the orthogonality relation ${\int }_{a_1}^{b_1}{\phi }_i(r){\phi }_j(r)\mathrm{d}r={\delta }_{ij}$ holds.

1. Derive an expression for ${\xi }_i$ in the Karhunen-Loève expansion.

Hint: Multiply throughout by ${\phi }_j(r)$, integrate with respect to $r$, and use the orthogonality relation.

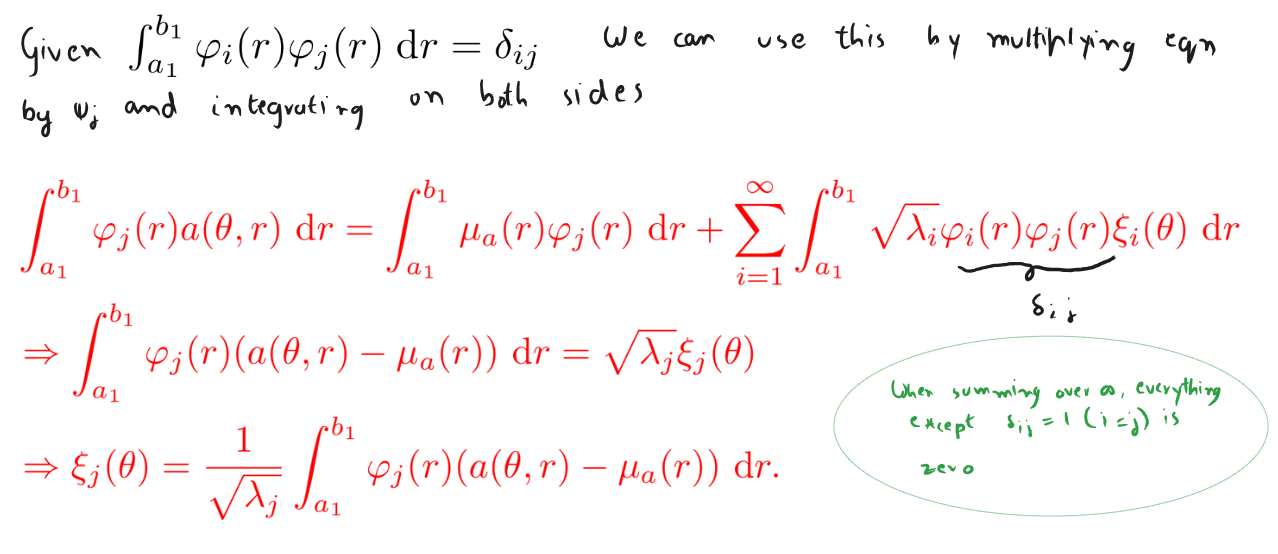
2. Express the covariance function of $a$ in terms of eigenvalues and eigenfunctions of the Karhunen-Loève expansion. You can assume that the ${\xi }_i$ are mean-free and orthogonal with unit variance.