K-means Algorithm

The k-means algorithm is an iterative method to partition N data points into K clusters. For two clusters, the process is as follows:

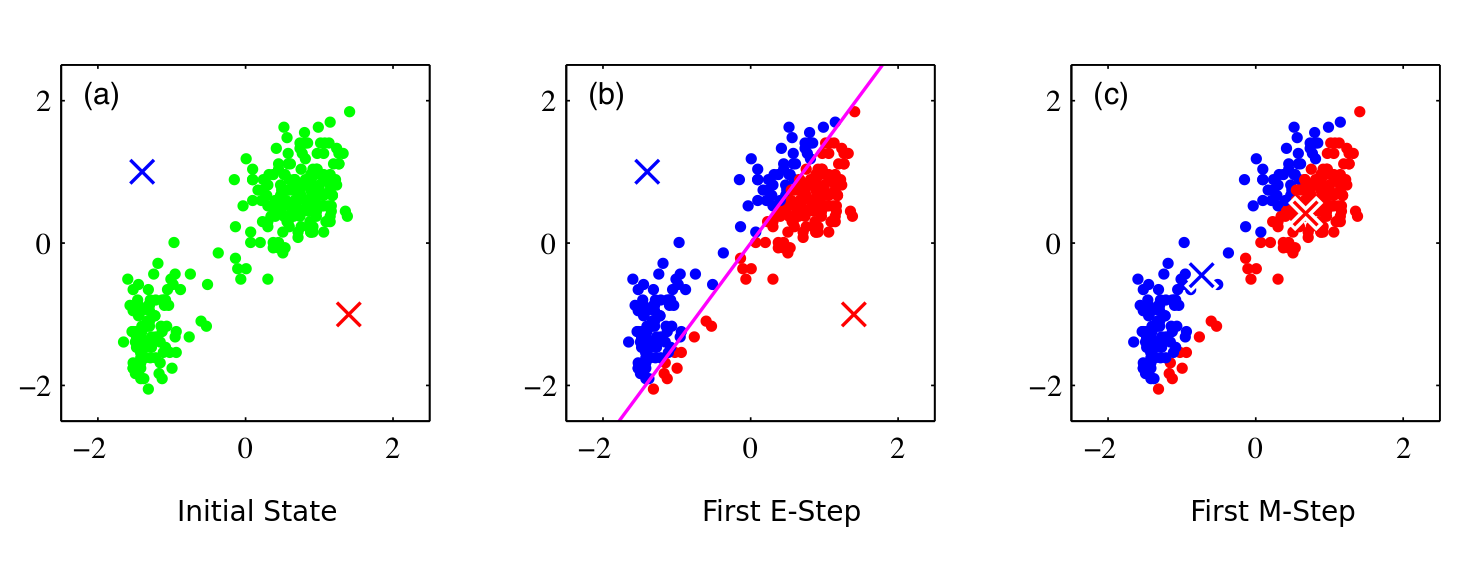
1. Initialization: Randomly initialize the positions of two prototypes (cluster centers), let’s call them the red ‘x’ and the blue ‘x’.
2. Assignment Step (E-step): Assign each data point to the nearest prototype. All points closer to the red ‘x’ become part of the red cluster, and all points closer to the blue ‘x’ become part of the blue cluster. This partitions the data space.
3. Update Step (M-step): Recalculate the position of each prototype by taking the mean (center) of all data points assigned to its cluster. The red ‘x’ moves to the center of the red data points, and the blue ‘x’ moves to the center of the blue data points.
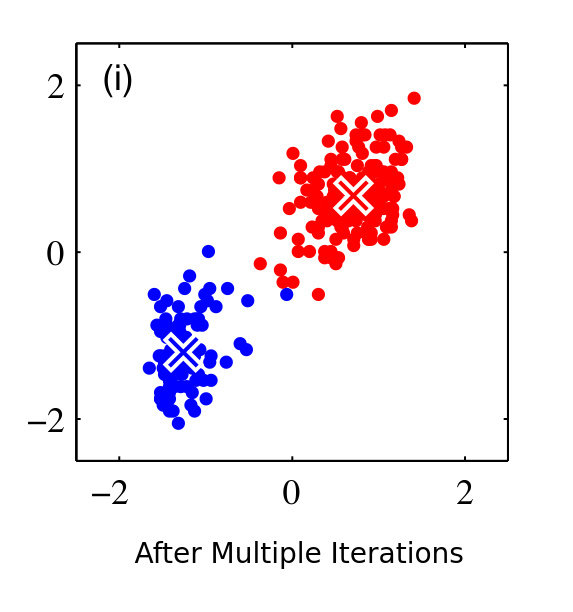
4. Repeat: Steps 2 and 3 are repeated until the cluster assignments no longer change, meaning the algorithm has converged to a solution.

Optimization Criteria

K-means minimizes the quantization error, which is the sum of the squared distances between each data point $x_n$ and its assigned cluster’s prototype $w_k$. The objective function $J$ is:

$J={\sum }_{n=1}^N{\sum }_{k=1}^K{r}_{nk}||x_n-w_k|{|}^2$

Where $r_{nk}$ is 1 if data point $x_n$ is assigned to cluster $k$, and $0$ otherwise.