Numerical Methods - Practice Test

Task 1

Solution

Constant means the degree is $0$

Task 2

Solution

230507 Quadrature - Derivation and Formulae Quadrature error estimation

• $f^{\prime \prime }(x)=12c_1{x}^2+6c_{2}x=-x^2+2x$
• Check: $f^{\prime \prime }(-1)=-3,f^{\prime \prime }(1)=1,f^{\prime \prime }(3)=-3$
• Therefore $M_2=3$

Error bound (in formulary)

$$|R(f)|\le \frac{(b-a{)}^3}{12}{M}_2$$ $$|R(f)|\le \frac{(3-(-1){)}^3}{12}\cdot 3=\frac{64}{12}\cdot 3=16$$

For $c_1=c_2=0,c_3,c_4\in \mathbb{R}$ : $f(x)=c_{3}x+c_4$ is a polynomial of degree $1$ .

Since the trapezoid rule has degree of accuracy 1, it integrates all polynomials of degree $\le 1$ exactly.

Therefore, the quadrature error is exactly 0 .

Exam relevance: Error estimation formulas are frequently tested!

Task 3

Solution

Part (a) - Romberg Extrapolation for Forward Difference Quotient

The forward difference quotient has the form:

$$f^{\prime }(x)\approx \frac{f(x+h)-f(x)}{h}$$

From Taylor expansion:

$$f(x+h)=f(x)+h{f}^{\prime }(x)+\frac{h^2}{2}{f}^{\prime \prime }(x)+O(h^3)$$

Rearranging, we have

$$\frac{f(x+h)-f(x)}{h}=f^{\prime }(x)+\stackrel{O(h)}{\overbrace{\frac{h}{2}{f}^{\prime \prime }(x)+O(h^2)}}$$

This shows the forward difference quotient has convergence order 1. Applying Romberg extrapolation Let $A(h)=\frac{f(x+h)-f(x)}{h}$ and $\frac{f^{\prime \prime }(x)}{2}=c$

Then we have

$$A(h)=f^{\prime }(x)+ch+O(h^2)$$

• $A(h)=f^{\prime }(x)+ch+O(h^2)$
• $A(h/2)=f^{\prime }(x)+c\frac{h}{2}+O(h^2)$

Using Romberg’s formula with $q=1$:

$$A_{new}=\frac{2A(h/2)-A(h)}{2-1}=2A(h/2)-A(h)=f^{\prime }(x)+O(h^2)$$

Convergence order 2.

Substituting to get the calculation formula:

$$Q_{new}=2\cdot \frac{f(x+h/2)-f(x)}{h/2}-\frac{f(x+h)-f(x)}{h}$$ $$=\frac{-3f(x)+4f(x+h/2)-f(x+h)}{h}$$

Common Mistakes

Why do we consider the full Taylor Polynomial? Because is acts as the Blueprint for the error. Note that in Romberg extrapolation is basically a clever trick to cancel out the errors.
Why expand up to $f^{\prime \prime }$ and not directly use the $O(h)$ notation? Same answer as above: We need the term so that we can cancel it out!

Part (b) - Numerical Approximations

For $f(x)=x^{-1}$ at $x=1$ with $h=1/2$:

• $f(1)=1$
• $f(3/2)=2/3$
• $f(1/2)=2$

Exact derivative: $f^{\prime }(x)=-x^{-2}$, so $f^{\prime }(1)=-1$

Forward difference quotient:

$$f^{\prime }(1)\approx \frac{f(3/2)-f(1)}{1/2}=-\frac{2}{3}$$

Romberg scheme from (a):

$$f^{\prime }(1)\approx \frac{-3f(1)+4f(5/4)-f(3/2)}{1/2}=-\frac{14}{15}$$

Central difference quotient:

$$f^{\prime }(1)\approx \frac{f(3/2)-f(1/2)}{2\cdot 1/2}=-\frac{4}{3}$$

Comparison with exact value $f^{\prime }(1)=-1$:

• Forward difference: $-2/3$ (error = $1/3$)
• Romberg scheme: $-14/15$ (error = $1/15$)
• Central difference: $-4/3$ (error = $1/3$)

The Romberg scheme provides the best approximation, as expected from its higher convergence order.

Task 4 (Nonlinear Equations)

Note: Newton’s method formulas are available in the formulary.

Part a) Derive Newton’s method from Taylor expansion (1 point)

Taylor expansion of $f(x)$ around point $x_k$:

$$f(x)=f(x_k)+f^{\prime }(x_k)(x-x_k)+O((x-x_k{)}^2)$$ $$f(x)\approx f(x_k)+f^{\prime }(x_k)(x-x_k)$$

To find the zero, we set this linear approximation equal to zero:

$$0=f(x_k)+f^{\prime }(x_k)(x-x_k)$$

Solving for $x$ gives us the next iterate:

$$x=x_k-\frac{f(x_k)}{f^{\prime }(x_k)}$$

Therefore, Newton’s method is:

$$\boxed{x_{k+1}=x_k-\frac{f(x_k)}{f^{\prime }(x_k)}}$$

Part b) Calculate two Newton steps (2 points)

For $f(x)=\frac{1}{4}{x}^2$, we have $f^{\prime }(x)=\frac{1}{2}x$ Starting from $x_0=4$:

$$x_1=x_0-\frac{f(x_0)}{f^{\prime }(x_0)}=2$$ $$x_2=x_1-\frac{f(x_1)}{f^{\prime }(x_1)}=1$$

Explanation: Newton’s method approximates $f$ by its tangent line at each iteration and finds where the tangent intersects the $x-$axi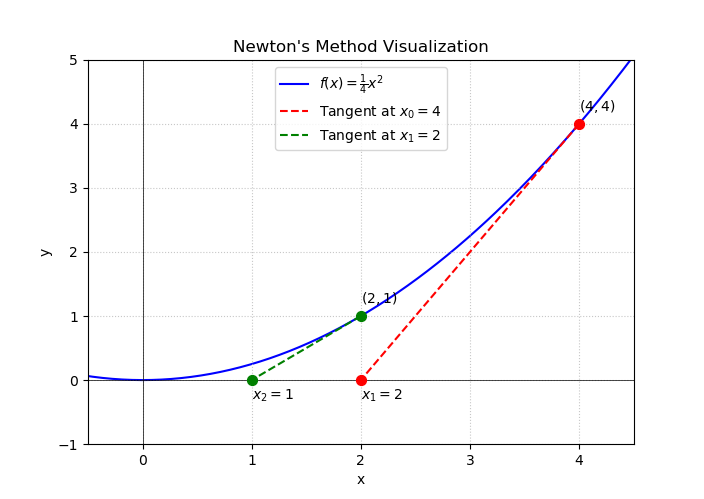s. Sketch should show parabola $f(x)=\frac{1}{4}{x}^2$, starting point $(4,4)$, tangent line at $x=4$ intersecting $x-$axis at $x=2$, then tangent at $x=2$ intersecting at $x=1$

Part c) Connection to Banach iteration and convergence order (2 points)

• Connection between Fixed Point Iteration & Newton’s Method

• Convergence order: The derivative of the iteration function is:

  $$g^{\prime }(x)=1-\frac{f^{\prime }(x{)}^2-f(x)f^{\prime \prime }(x)}{[f^{\prime }(x){]}^2}=\frac{f(x)f^{\prime \prime }(x)}{[f^{\prime }(x){]}^2}$$

At the root $x\ast$ where $f(x\ast )=0$:

$$g^{\prime }(x\ast )=\frac{f(x\ast )f^{\prime \prime }(x\ast )}{[f^{\prime }(x\ast ){]}^2}=0$$

Since $g^{\prime }(x\ast )=0$, Newton’s method has quadratic convergence (order 2) near the root, assuming $f^{\prime }(x\ast )\ne 0$ and $f^{\prime \prime }(x\ast )$ exists.

This means the error approximately squares in each iteration: $|x_{k+1}-x\ast |\approx C|x_k-x\ast {|}^2$ for some constant $C$

Task 5

Solution

a) Maximal Step Size and System Property

To find the maximal step size for the explicit Euler method, we first need the eigenvalues of the system matrix $A=-\left(\begin{array}{cc}2& 1\\ 0& 2\end{array}\right)$. Since the matrix is upper triangular, the eigenvalues are its diagonal entries:

$${\lambda }_1=-2\text{and}{\lambda }_2=-2$$

The explicit Euler method is stable if for all eigenvalues $\lambda$, the step size $h$ satisfies the condition:

$$\boxed{|1+h\lambda |\le 1}$$

Since our eigenvalues are real and identical, we only need to solve for $\lambda =-2$:

$$|1-2h|\le 1$$

This inequality can be split into two parts:

$$-1\le 1-2h\le 1$$

Solving for $h$:

$$-2\le -2h\le 0⟹1\ge h\ge 0$$

The maximal step size is $h_{max}=1$.

A property of this system is that it is not stiff. A system is considered stiff if the ratio of the largest to the smallest absolute value of the real parts of the eigenvalues is large. Here, the ratio is $|-2|/|-2|=1$, which is the opposite of stiff.

b) Two Steps with h = 0.5

The explicit Euler method is given by the formula:

$$y_{i+1}=y_i+h_{i}f(t_i,y_i)$$ $$q_{i+1}=q_i+hA{q}_i$$

Given $q_0=\left(\begin{array}{c}1\\ 4\end{array}\right)$, $h=0.5$, and $A=\left(\begin{array}{cc}-2& -1\\ 0& -2\end{array}\right)$.

Step 1: Calculate $q_1$ First, we calculate the product $A{q}_0$:

$$A{q}_0=\left(\begin{array}{cc}-2& -1\\ 0& -2\end{array}\right)\left(\begin{array}{c}1\\ 4\end{array}\right)=\left(\begin{array}{c}-6\\ -8\end{array}\right)$$

Now we find $q_1$:

$$q_1=q_0+hA{q}_0=\left(\begin{array}{c}1\\ 4\end{array}\right)+0.5\left(\begin{array}{c}-6\\ -8\end{array}\right)=\left(\begin{array}{c}-2\\ 0\end{array}\right)$$

Step 2: Calculate $q_2$ First, we calculate the product $A{q}_1$:

$$A{q}_1=\left(\begin{array}{cc}-2& -1\\ 0& -2\end{array}\right)\left(\begin{array}{c}-2\\ 0\end{array}\right)=\left(\begin{array}{c}4\\ 0\end{array}\right)$$

Now we find $q_2$:

$$q_2=q_1+hA{q}_1=\left(\begin{array}{c}-2\\ 0\end{array}\right)+0.5\left(\begin{array}{c}4\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right)$$

After two steps, the solution is $q_2=\left(\begin{array}{c}0\\ 0\end{array}\right)$.

Task 5B

Consider differential equation:

$$\dot{q}(t)=-\left(\begin{array}{cc}2& 1\\ 0& 2\end{array}\right)q(t),q(0)=\left(\begin{array}{c}1\\ 4\end{array}\right).$$

a) The Crank-Nicolson method is known to be A-stable. Explain what A-stability implies for the choice of step size $h$ when solving this particular system. Is this method a good choice for this system?

b) Perform one step of the Crank-Nicolson method with a step size of $h=1.0$ to find the approximation $q_1$.

a) A-Stability and Method Suitability

A numerical method is A-stable if its stability region contains the entire left half of the complex plane, $\{z\in \mathbb{C}:\text{Re}(z)\le 0\}$ . The Crank-Nicolson method is A-stable.

The eigenvalues of the system matrix are ${\lambda }_1={\lambda }_2=-2$, which are on the negative real axis (i.e., in the left half-plane). Because the method is A-stable, the term $h\lambda$ will lie within the stability region for any positive step size $h>0$.

This means that for the Crank-Nicolson method, there is no upper limit on the step size $h$ imposed by stability. The choice of $h$ can be based purely on the desired accuracy of the solution. This makes it a very robust and good choice, especially for stiff differential equations.

b) One Step of Crank-Nicolson with h = 1.0

$$y_{i+1}=y_i+\frac{h_i}{2}[f(t_i,y_i)+f(t_{i+1},y_{i+1})]$$

The Crank-Nicolson method for a system $\dot{q}=Aq$ is given by:

$$q_{i+1}=q_i+\frac{h}{2}(A{q}_i+A{q}_{i+1})$$

To solve for the unknown vector $q_{i+1}$, we must first rearrange the formula into a linear system of equations:

$$q_{i+1}-\frac{h}{2}A{q}_{i+1}=q_i+\frac{h}{2}A{q}_i⟹\left(I-\frac{h}{2}A\right)q_{i+1}=\left(I+\frac{h}{2}A\right)q_i$$

Given $h=1.0$, $A=\left(\begin{array}{cc}-2& -1\\ 0& -2\end{array}\right)$, and $q_0=\left(\begin{array}{c}1\\ 4\end{array}\right)$.

1. Set up the linear system: First, we compute the matrices on the left and right sides.

• Left-Hand Side Matrix:

  $$I-\frac{h}{2}A=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)-0.5\left(\begin{array}{cc}-2& -1\\ 0& -2\end{array}\right)=\left(\begin{array}{cc}2& 0.5\\ 0& 2\end{array}\right)$$

• Right-Hand Side Vector:

  $$\left(I+\frac{h}{2}A\right)q_0=\left(\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)+0.5\left(\begin{array}{cc}-2& -1\\ 0& -2\end{array}\right)\right)\left(\begin{array}{c}1\\ 4\end{array}\right)=\left(\begin{array}{c}-2\\ 0\end{array}\right)$$

The system to solve for $q_1$ is:

$$\left(\begin{array}{cc}2& 0.5\\ 0& 2\end{array}\right)q_1=\left(\begin{array}{c}-2\\ 0\end{array}\right)$$

2. Solve for $q_1$: Let $q_1=\left(\begin{array}{c}x\\ y\end{array}\right)$. We can solve the system using back substitution.

• From the second row: $2y=0⟹y=0$.
• From the first row: $2x+0.5y=-2⟹2x+0=-2⟹x=-1$.

The solution after one step is:

$$q_1=\left(\begin{array}{c}-1\\ 0\end{array}\right)$$

Task 5C

Consider the differential equation:

$$\dot{q}(t)=-\left(\begin{array}{cc}2& 1\\ 0& 2\end{array}\right)q(t),q(0)=\left(\begin{array}{c}1\\ 4\end{array}\right).$$

a) The implicit Euler method is known to be A-stable. Explain what this implies for the choice of step size $h$ when solving this system.

b) Perform one step of the implicit Euler method with a step size of $h=1.0$ to find the approximation $q_1$.

Solution

a) A-Stability and Method Suitability

A numerical method is A-stable if its stability region contains the entire left half of the complex plane, $\{z\in \mathbb{C}:\text{Re}(z)\le 0\}$. The implicit Euler method is A-stable.

The eigenvalues of the system matrix are $\lambda =-2$, which are in the left half-plane. Because the method is A-stable, the term $h\lambda$ will always lie inside the stability region for any positive step size $h>0$.

This means there is no upper limit on the step size $h$ for stability. The choice of $h$ can be based purely on the desired accuracy of the solution, making the method very robust.

b) One Step of Implicit Euler with h = 1.0

$$y_{i+1}=y_i+h_{i}f(t_{i+1},y_{i+1})$$

The implicit Euler method is given by the formula:

$$q_{i+1}=q_i+hA{q}_{i+1}$$

To solve for the unknown vector $q_{i+1}$, we must rearrange the formula into a linear system of equations:

$$q_{i+1}-hA{q}_{i+1}=q_i⟹(I-hA)q_{i+1}=q_i$$

Given $h=1.0$, $A=\left(\begin{array}{cc}-2& -1\\ 0& -2\end{array}\right)$, and $q_0=\left(\begin{array}{c}1\\ 4\end{array}\right)$.

1. Set up the linear system: First, we compute the matrix on the left-hand side:

$$I-hA=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)-1.0\left(\begin{array}{cc}-2& -1\\ 0& -2\end{array}\right)=\left(\begin{array}{cc}3& 1\\ 0& 3\end{array}\right)$$

The system to solve for $q_1$ is:

$$\left(\begin{array}{cc}3& 1\\ 0& 3\end{array}\right)q_1=\left(\begin{array}{c}1\\ 4\end{array}\right)$$

2. Solve for $q_1$: Let $q_1=\left(\begin{array}{c}x\\ y\end{array}\right)$. We can solve the system using back substitution.

• From the second row: $3y=4⟹y=4/3$.
• From the first row: $3x+y=1⟹3x+4/3=1⟹3x=-1/3⟹x=-1/9$.

The solution after one step is:

$$q_1=\left(\begin{array}{c}-1/9\\ 4/3\end{array}\right)$$

Task 6

a) Definition and Explanation of Consistency

Consistency for a one-step method means that the numerical scheme genuinely represents the differential equation in the limit as the step size $h$ approaches zero.

In other words for it answers the question “For an an infinitesimally small step, does the given method behave like the actual differential equation?”

This is measured with the local truncation error, $\tau (t,h)$, which is the error the method makes in a single step, assuming the starting point was perfectly accurate.

A method is consistent if this error vanishes as the step size shrinks to zero. The order of consistency, $q$, tells us how fast the error disappears, with the error being proportional to $h^q$.

---

b) Order of Consistency Calculation

Euler Method

The Euler method is defined by $y_{i+1}=y_i+hf(t_i,y_i)$. [cite_start]The increment function is $\Phi (t,y,h)=f(t,y)$[cite: 589].

1. Set up the truncation error formula:

   $$\tau (t,h)=\frac{y(t+h)-y(t)}{h}-\Phi (t,y(t),h)=\frac{y(t+h)-y(t)}{h}-f(t,y(t))$$

2. Use Taylor Series: We expand $y(t+h)$ around $t$:

   $$y(t+h)=y(t)+h{y}^{\prime }(t)+\mathcal{O}(h^2)$$

3. Substitute and Simplify:

   $$\tau (t,h)=\frac{(y(t)+h{y}^{\prime }(t)+\mathcal{O}(h^2))-y(t)}{h}-f(t,y(t))$$ $$\tau (t,h)=y^{\prime }(t)+\mathcal{O}(h)-f(t,y(t))$$

   Since $y^{\prime }(t)=f(t,y(t))$, the leading terms cancel:

   $$\tau (t,h)=\mathcal{O}(h)$$

The local truncation error is of the first order in $h$. Therefore, the Euler method has an order of consistency of 1.

Euler-Heun Method

[cite_start]The Euler-Heun method’s increment function is $\Phi (t,y,h)=\frac{1}{2}[f(t,y)+f(t+h,y+hf(t,y))]$[cite: 591].

1. Set up the truncation error formula:

   $$\tau (t,h)=\frac{y(t+h)-y(t)}{h}-\frac{1}{2}[f(t,y(t))+f(t+h,y(t)+hf(t,y(t)))]$$

2. Use Taylor Series for all terms:

   • Left Part: We expand $y(t+h)$ to a higher order: $y(t+h)=y(t)+h{y}^{\prime }(t)+\frac{h^2}{2}{y}^{\prime \prime }(t)+\mathcal{O}(h^3)$. This gives:

     $$\frac{y(t+h)-y(t)}{h}=y^{\prime }(t)+\frac{h}{2}{y}^{\prime \prime }(t)+\mathcal{O}(h^2)$$

   • Right Part: We use a multivariate Taylor expansion for the second $f$ term:

     $$f(t+h,y+hf)=f(t,y)+h\frac{\partial f}{\partial t}+(hf)\frac{\partial f}{\partial y}+\mathcal{O}(h^2)$$

     So the full increment function is:

     $$\Phi (t,y,h)=\frac{1}{2}[f+(f+h\frac{\partial f}{\partial t}+hf\frac{\partial f}{\partial y}+\mathcal{O}(h^2))]=f+\frac{h}{2}\left(\frac{\partial f}{\partial t}+f\frac{\partial f}{\partial y}\right)+\mathcal{O}(h^2)$$

3. Substitute and Simplify: Using $y^{\prime }=f$ and $y^{\prime \prime }=\frac{\partial f}{\partial t}+f\frac{\partial f}{\partial y}$, the increment function becomes:

   $$\Phi (t,y(t),h)=y^{\prime }(t)+\frac{h}{2}{y}^{\prime \prime }(t)+\mathcal{O}(h^2)$$

   Now, we substitute everything back into the truncation error formula:

   $$\tau (t,h)=\left(y^{\prime }(t)+\frac{h}{2}{y}^{\prime \prime }(t)+\mathcal{O}(h^2)\right)-\left(y^{\prime }(t)+\frac{h}{2}{y}^{\prime \prime }(t)+\mathcal{O}(h^2)\right)=\mathcal{O}(h^2)$$

The local truncation error is of the second order in $h$. [cite_start]Therefore, the Euler-Heun method has an order of consistency of 2[cite: 645].