Polynomial Chaos Expansion

Definition

It is a way to express Random Variables as a linear expansion using Orthogonal polynomials of simpler random variables (called the germ)

Formula

Let $X$ be a random variable with arbitrary $\mathrm{PDF}{f}_X$, for which the mean value and variance exist $(\mathbb{E}[X],\mathbb{V}[X]<\infty )$. Using the generalized Polynomial Chaos (gPC) Expansion

$$X(\theta )=\sum _{i=0}^{\infty }{q}_i{\Phi }_i(\xi (\theta ))$$ $$\boxed{X=\sum _{i=0}^{\infty }{q}_i{\Phi }_i(\xi )}$$

Where,

• $q_i$ are deterministic coefficients (also called PC coefficients). They encode important information about distribution and act as weights.
• ${\Phi }_i$ are Orthogonal Polynomials (e.g.Hermite polynomials)
• $\xi \sim \mathcal{N}(0,1)$ is the germ
• Each $\xi$ term is called a germ.
• The Polynomials are orthogonal to the the germ.

Note: The choice of the Orthogonal Polynomials (${\Phi }_i$), depends on the distribution of the germ $\xi$. According to the Askey Scheme

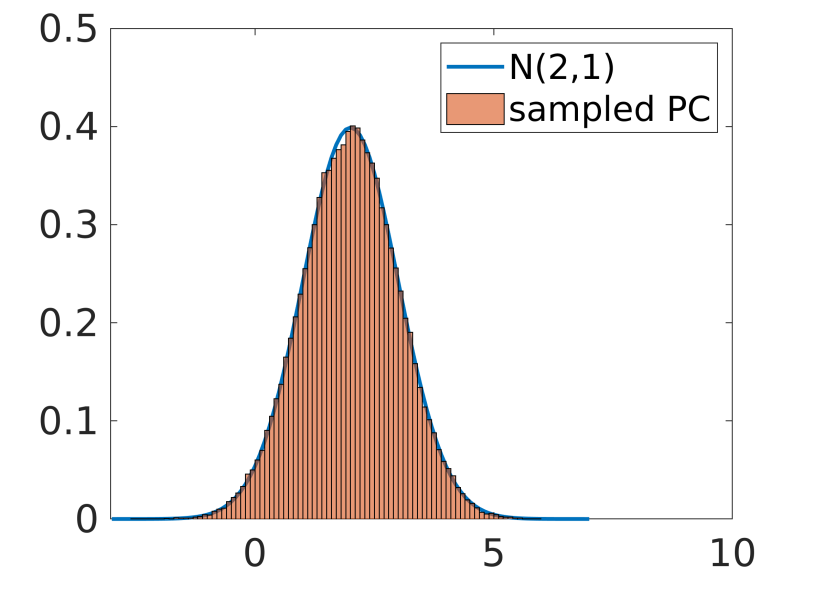
Example

Random Variable

$$X\sim \mathcal{N}(2,1)$$

Polynomial Chaos expansion

$$X=2+\xi$$

Where, $\xi \sim \mathcal{N}(0,1)$