Romberg's Extrapolation Method

Use case

It is used to improve the accuracy of a numerical method to a higher order by combining results from different step sizes. It does this by eliminating the lower-order error terms from the asymptotic error expansion.

Mathematically

For a numerical method with approximation $A(h)$ of the exact value, where the error has convergence order $q$:

$A_{new}=\frac{2^{q}A(h/2)-A(h)}{2^q-1}$

Here,

• $q$ is the convergence order of the original method
• The new approximation $A_{new}$ has convergence order $q+1$ (or $q+2$ for methods with only even error terms)

Note: Each extrapolation step increases the convergence order. For integration methods like trapezoid rule, the order increases by 2 in each iteration as the expansion contains only even powers of $h$.

Examples:

• Trapezoid rule ($q=2$): $A_{new}=\frac{4A(h/2)-A(h)}{3}$
• Simpson’s rule ($q=4$): $A_{new}=\frac{16A(h/2)-A(h)}{15}$

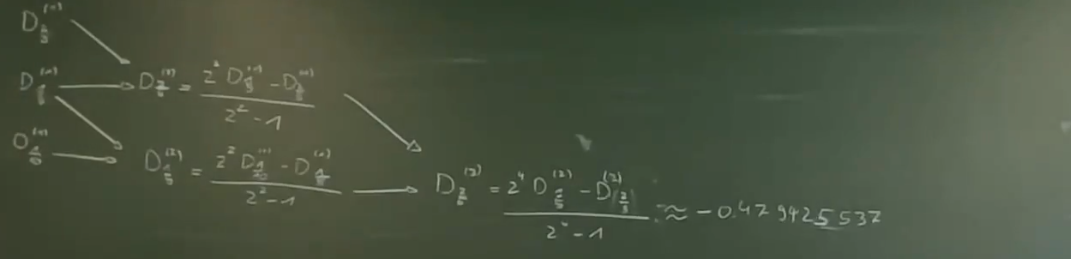
Quadrature Method	Order of Convergence
Left Hand Rule	$O(h)$
Midpoint Rule	$O(h^2)$
Trapezoidal Rule	$O(h^2)$
Simpson’s Rule	$O(h^4)$

---

Derivation of the Romberg Extrapolation

Consider a numerical method with error expansion:

$$A(h)=y_{\text{exact }}+C_1{h}^q+C_2{h}^{q+1}+C_3{h}^{q+2}+\dots$$

The dominant error term is $C_1{h}^q$ (lowest power, largest contribution). Elimination Process With two approximations:

• $A(h)=y_{\text{exact }}+C_1{h}^q+O\left(h^{q+1}\right)$
• $A(h/2)=y_{\text{exact }}+C_1(h/2{)}^q+O\left(h^{q+1}\right)$

Step 1: Multiply the second equation by $2^q$ :

$$2^{q}A(h/2)=2^q{y}_{\text{exact }}+\underset{\text{eliminate}}{\underbrace{C_1{h}^q}}+O\left(h^{q+1}\right)$$

Step 2: Subtract the first equation:

$$2^{q}A(h/2)-A(h)=\left(2^q-1\right)y_{\text{exact }}+O\left(h^{q+1}\right)$$

Step 3: Solve for $y_{\text{exact }}$ :

$$y_{\text{exact }}=\frac{2^{q}A(h/2)-A(h)}{2^q-1}+O\left(h^{q+1}\right)$$

Result

The $C_1{h}^q$ term cancels out completely, leaving only higher-order error terms $O\left(h^{q+1}\right)$. This is what we mean by “eliminating” the lower-order error term.

Example For trapezoid rule with $q=2$ :

• Original error: $O\left(h^2\right)$
• After extrapolation: $O\left(h^4\right)$ (the $h^2$ term is eliminated)

The approximation becomes much more accurate because we’ve removed the largest source of error.