Optimization problem for an SVM dealing with Separable Dataset

An SVM for a linearly separable dataset finds the single best hyperplane that separates the two classes. It achieves this by solving a specific, constrained optimization problem.

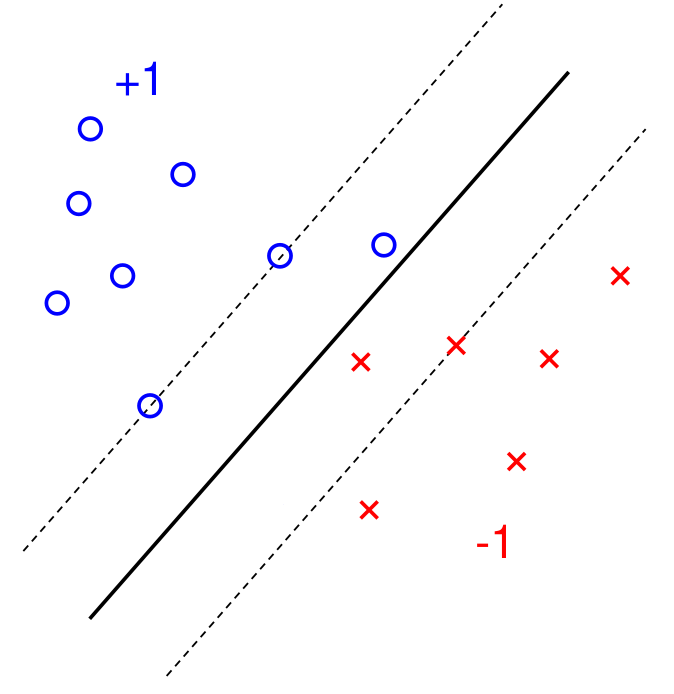The goal is to find the decision hyperplane that maximizes the margin. The margin is the buffer between the two closest points of the opposing classes

Note: In the SVM Classification shown. Some relaxation has been applied. Hence you have a few points inside the margin.

Optimization Problem

• Minimize:

  $$\underset{\mathbf{w},b}{\min }\left(\frac{1}{2}{||w||}^2\right)$$

• Subject to the constraint:

  $$y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1\text{for all training points }i$$

Where:

• $\mathbf{w}$ and $b$ define the decision hyperplane.
• ${\mathbf{x}}_i$ is a training data point.
• $y_i$ is the class label for that point (+1 or -1).

Breakdown of the Constraint Formula

The constraint $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1$ is the core of the SVM. It ensures that every data point is not only classified correctly but also stays out of the margin.

1. $({\mathbf{w}}^T{\mathbf{x}}_i+b)$ — The Decision Function

   • This part calculates a “score” for each data point ${\mathbf{x}}_i$.
   • The sign of the score determines which side of the decision hyperplane the point lies on. A score of 0 means it’s exactly on the line.

2. $y_i\cdot (\dots )$ — The Correctness Check

   • The class label $y_i$ is either +1 or -1.
   • Multiplying the score by the true label checks for correctness. If the point is on the right side, the product will be positive. If it’s on the wrong side, the product will be negative.

3. $\ge 1$ — Enforcing the Margin

   • This is the crucial part. Instead of just requiring the product to be positive, the SVM insists it must be at least 1.
   • This establishes the margin boundaries at ${\mathbf{w}}^T\mathbf{x}+b=1$ and ${\mathbf{w}}^T\mathbf{x}+b=-1$.
   • This constraint forces all data points to be on or outside of this margin, creating the empty street that the SVM seeks to maximize.

Key Takeaway: The constraint elegantly combines the requirement for correct classification with the requirement for a minimum distance from the decision boundary.

Support Vectors

The data points for which the constraint is an exact equality (i.e., $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)=1$) are called support vectors. They “support” i.e define the final position of the hyperplane.