Kernel-Based Method for Supervised non-Parametric Estimation (Parzen Windows)

In this method we fix a volume $V_T$ of a region around a point $x$ and then count the number of data samples, $k_T$, that fall within that volume. The volume is typically decreased as the total number of samples, T, increases.

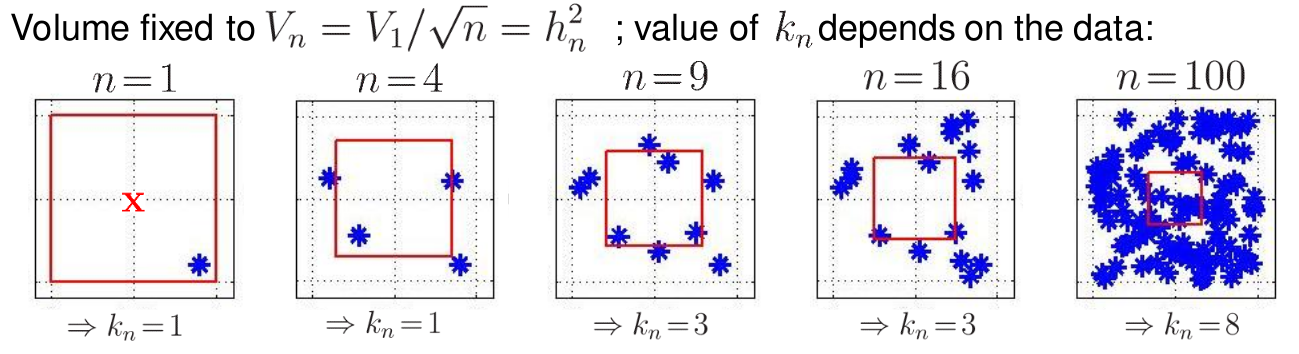
Drawbacks

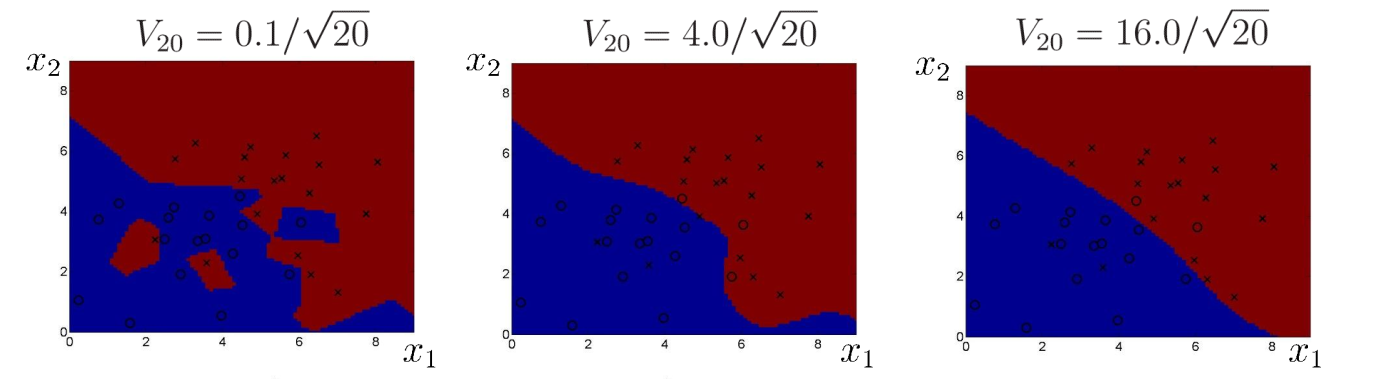
A key challenge is choosing an appropriate volume (or bandwidth) for the kernel. The optimal volume can vary depending on the local density of the data:

• Small Volume: This works well in regions with high data density, as it captures fine details of the distribution. However, in sparse regions, it can lead to noisy and inaccurate estimates.
• Large Volume: This is better for regions with low data density, as it smooths out the estimate and avoids zero probabilities. However, in dense regions, it can over-smoothen the distribution, blurring important decision boundaries.

Solution

We know that

• Small Volume → Good for high density regions
• Large Volume → Good for low density regions

Therefore, a better approach is to make the volume data-dependent. This means the volume would be smaller in regions with high data density and larger in regions with low data density.